Cholesky 分解（四）

13 Dec 2016 - 4 minute read

上一回里我们看到了一个比较直观的结论：选择尽可能稀疏的行和列优先消去，得到的分解会比较稀疏。现在我们将问题换一种方式表达，并在这种表达下再次分析我们的结论。

我们知道对称的矩阵可以用一个（带边权）的无向图表示，特定的行列对应着特定的顶点。在我们交换行列时，保持与定点的对应关系跟随行列变化的话，那么交换得到的矩阵和原始的矩阵对应着完全相同的图。

这样，我们在矩阵里选择特定的行列并消去的过程可以变成在矩阵对应的无向图中选择一个特定顶点（并消去）的过程。

还是以上文图中的 A 为例，这个矩阵对应了如下的无向图：

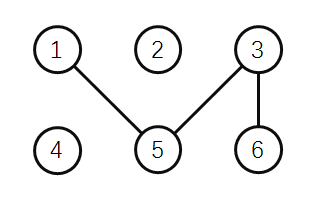
在矩阵中选取特定的行列进行消去的过程，在无向图表示下则是“将对应的节点删除，并将其尚未消去的邻居节点两两连接，形成完全子图（clique）”。

在上图中，节点 2 和 4 很明显是独立的，这就意味着即使将它们消去，也不会影响剩余的图的结构。类似地，节点 1 和 6 只有一个邻居，消去它们同样不会引入新的边，也就是不会在分解中产生新的非零元素。然而节点 3 和 5 则不同。我们同样以节点 5 为例，为了消去它，需要在节点 1 和 3 之间引入新的边。在前文里我们看到了，如果 Pivot 在了第 5 行第 5 列，则消去之后会多出两个新的非零元。

在这种图论的表示下，寻找尽可能稀疏化 Cholesky 分解的置换矩阵变为了寻找尽可能不引入新的边的顶点消去顺序。在这一思路的引导下，最直观的一个策略便是优先消去度数尽可能低的节点。因此采用了这类策略的置换方法便得名 Minimum Degree Reordering 方法。

矩阵的 Schur 补

12 Dec 2016 - 6 minute read

在线性方程求解中，有一个重要的技巧叫做 Schur 补。

设分块矩阵 $A=\begin{pmatrix}A_{11} & A_{12} \\ A_{21} & A_{22}\end{pmatrix}$ ，其中 $A_{11}$ 可逆。在线性方程 $Ax=b$ 中，对 $x$ 和 $b$ 以兼容的方式分块，可以得到：

\[\begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2\end{pmatrix}.\]

如果对 $A$ 进行高斯消元，利用块状行变换消去 $A_{21}$ ，上面的等式可以变形为：

\[\begin{pmatrix} A_{11} & A_{12} \\ 0 & A_{22}-A_{21}A_{11}^{-1}A_{12} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2-A_{21}A_{11}^{-1}b_1 \end{pmatrix}.\]

这样，第二行就变成了一个变量更少的线性方程：

\[(A_{22}-A_{21}A_{11}^{-1}A_{12})x_2 = b_2- A_{21}A_{11}^{-1}b_1.\]

在一些场合，可以先求解这一线性方程得到 $x_2$ ，然后代入到第一行再求解出 $x_1$ 。

这里出现了一个矩阵 $S = A_{22}-A_{21}A_{11}^{-1}A_{12}$ ，它被称为矩阵 $A$ 关于 $A_{11}$ 的 Schur 补，也记作 $A/A_{11}$，而这个方程求解的方法被称为 Schur 补技巧。

如果使用 Schur 补技巧来求解上面的方程，通常要求 $A_{11}$ 可逆且比较容易求逆。在一些问题中，我们的矩阵可以分块使得 $A_{11}$ 为（块）对角矩阵，这样允许我们很容易求出 $A_{11}^{-1}$ 。此外，其它的分块应当充分稀疏，从而允许我们加速 Schur 补的计算和求解新的线性系统。如果 $A_{11}$ 很大，对应着 Schur 补比较小，即使它相对更加稠密，求解的开销也会远远小于直接求解整个问题。

Cholesky 分解（三）

11 Dec 2016 - 6 minute read

上文我们提到了 Cholesky 分解面临的一个问题，就是对于一些形状的矩阵存在的过度 fill-in 。我们举了两个具体的例子：一个左上箭头形的矩阵和右下箭头形的矩阵。其中，对左上箭头形的矩阵的 Cholesky 分解将得到非常稠密的结果；而对右下箭头形的矩阵的分解则保持了原始的稀疏性。

那么如果一个方程 $Ax=b$ 中的 $A$ 碰巧是左上箭头形状，我们还能使用 Cholesky 分解来加快求解吗？坏消息是：直接 Cholesky 分解的话，得到的将会是稠密的线性系统，计算量会严重增大。好消息是：我们可以通过调整变量的顺序，也就是调整矩阵的行和列，将它变成更加喜闻乐见的（右下箭头）形状。

先来介绍一下更一般的结论：假设 $P$ 是一个置换矩阵（Permutation Matrix），可以通过求解 $PAP^T Px = Pb$ 来得到方程 $Ax = b$ 的解。而通过选择合适的 $P$ ，矩阵 $M = PAP^T$ 的 Cholesky 分解可能比 $A$ 本身的 Cholesky 分解更加稀疏。

为了说明这一点，我们来看看矩阵本身的稀疏模式如何影响 Cholesky 分解的稀疏性。首先，我们忽略矩阵中具体的数值，仅将非零的元素标记出来，得到一个着色的块图，例如下图中的 A 。

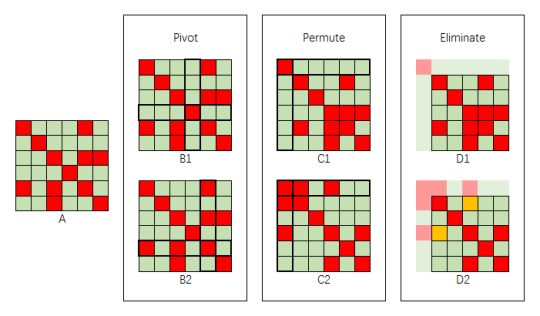
根据我们在系列第一篇文章中介绍的 Cholesky 分解算法，我们总是先求出结果的第一行第一列，然后在剩余的部分中减去第一列和第一行的乘积。因此，我们先在矩阵中选择（Pivot）一个目标的行列，将它移动（Permute）到首行首列，然后将它从剩余的部分中去除（Eliminate）。对剩余的部分，我们可以如法炮制继续下去。为了简化讨论，我们还假设计算中不存在任何因为数值舍入产生零的情况。

在上图中，我们展示了两种 Pivot 策略，B1 选择了第 4 行第 4 列，而 B2 则选择了第 5 行第 5 列。随后，将对应的行和列 Permute 到行列首，得到了 C1 和 C2 。

在其后的 Eliminate 中，这两种选择便表现出了差异：对于 B1 的 Pivot 方式，在进行 Eliminate 时，并不会对剩余的部分产生任何的影响。而 B2 的 Pivot 方式导致 C2 中首行首列存在非零元，这使得在 Eliminate 时，出现了引入新的非零元的机会。D2 中，我们用金色格点高亮了这两个新出现的非零元。

B1 相比 B2 的聪明之处是比较容易看出来的：B1 所在的行和列都是尽可能稀疏的，这样就大大降低了在 Eliminate 过程中引入新的非零元的机会。

RefBLAS is Slow

10 Dec 2016 - 4 minute read

很多的数值应用在核心部分都依赖快速的线性代数计算，BLAS 为这些线性代数计算提供了基本的 Building Block 。然而当前存在着非常多的 BLAS 实现，其中作为参考实现的是 netlib 的 Reference BLAS（我们简称 RefBLAS）。最近发现我们的一些项目中，为了偷懒直接使用了 RefBLAS 。这种做法其实是非常不好的。

RefBLAS 采用了 FORTRAN 语言实现，其作用是明确了 BLAS 的接口定义和行为。但是 FORTRAN 在当今已经不是主流语言了，甚至在 Windows 平台上缺少高效且免费的 FORTRAN 编译器。

RefBLAS 的实现是非常通用的，这就意味着它不会照顾到具体平台的具体特性，这其中就包括了寄存器使用、超标量加速、缓存预存取甚至专用数值指令等等可以带来巨大性能提升的特性。仅仅使用 RefBLAS 的话，等于是将优化寄托于编译器。

随着如今编译器的发展，使用纯 C 语言编写的 BLAS 早就已经赶上甚至超过了 RefBLAS 的性能。也就是说，即使不采用更加针对性的优化，RefBLAS 相较于 C 编写的 BLAS 也没有特别的优势。

进一步的，当各种针对特定计算/访问模式的优化被加入之后，整体效率的提升就更加可观了！BLAS 在各种数值程序中处在非常核心的位置，在计算中占据了相当大的一部分比例，使用 RefBLAS 造成的性能浪费将会是非常严重的。

结论就在标题中了，RefBLAS 是很慢的，绝不能因为它的代码很容易下载到，就使用它。

下面列举一些先进的 BLAS 实现：

• Intel MKL (商业软件，且仅在 Intel CPU 上有最佳性能)
• BLIS
• ulmBLAS
• OpenBLAS
• ATLAS

Cholesky 分解（二）

09 Dec 2016 - 6 minute read

Cholesky 有很多用途，其中之一是求解形如 $LL^T x = Ax = b$ 的线性方程。各类最小二乘算法中，经常会涉及到求解这类问题。

现实中，矩阵 $A$ 通常会根据问题性质具有不同的结构。这些结构有一个共同的特点，就是维度很高的同时，非零元个数很少。也就是说 $A$ 经常是稀疏矩阵。

对于稀疏矩阵的计算，我们可以采用更加高效的算法，这些算法的最原始思路便是跳过所有零元。对于 Cholesky 分解，情况也毫不例外。但是经验告诉我们：不同的稀疏模式， Cholesky 分解后的结果很有可能在稀疏性上有很大的差别。有的稀疏矩阵在分解后会得到稠密的下三角阵。这种现象被称为 fill-in 。

我们举两个例子来说明这个问题：

\[\begin{aligned} A &=\begin{pmatrix} 1 & -1 & -1 & -1 \\ -1 & 2 & & \\ -1 & & 3 & \\ -1 & & & 4 \end{pmatrix} &\mathrm{chol}(A) &=\begin{pmatrix} 1 & & & \\ -1 & 1 & & \\ -1 & -1 & 1 & \\ -1 & -1 & -1 & 1 \end{pmatrix}, \\ B &= \begin{pmatrix} 1 & & & 1 \\ & 1 & & 1 \\ & & 1 & 1 \\ 1 & 1 & 1 & 4 \end{pmatrix} &\mathrm{chol}(B) &=\begin{pmatrix} 1 & & & \\ & 1 & & \\ & & 1 & \\ 1 & 1 & 1 & 1 \end{pmatrix}. \end{aligned}\]

上面的例子里，$A$ 和 $B$ 具有相同个数的非零元，但在经过 Cholesky 分解后，一个得到的是稠密的下三角矩阵，另一个则保持了与原始矩阵相同的稀疏特性。